Using Existing RGB Color Spaces with Updated Color Matching Functions
Experiments with color matching functions and display profiles
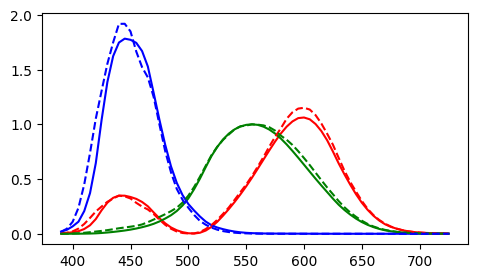
A comparison of old and new color matching functions.
The CIE 1931 XYZ color space is the basis of all additive RGB color spaces. While its color matching functions (CMFs) are a very close estimate of human perception, more accurate functions have been developed. Because common standard RGB spaces like sRGB or P3 are defined with the 1931 color space they cannot be used directly with the updated color space. This is because the XYZ coordinates of a color are different in each version.
Functions and Chromaticity Diagram
I am using the cvrl 2012 functions, I believe they are the same as the proposed 2015 CIE functions. I will refer to this as the “updated” or “new” observer/color space.
Plot of functions. New is dashed lines.
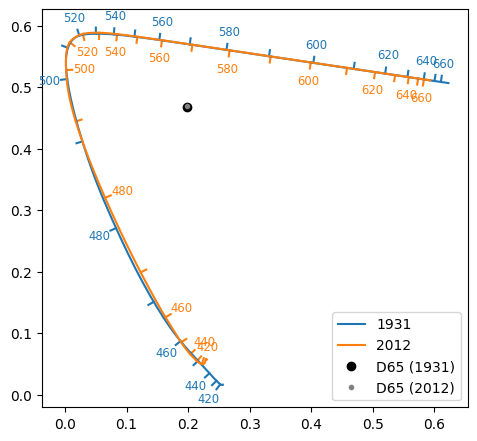
uv chromaticity diagram. Showing each spectral locus and wavelengths in nanometers.
Chromaticity Coordinates of some common RGB color spaces
rec 2020
| x | y | wavelength | |
|---|---|---|---|
| red | 0.708 | 0.292 | 630 nm |
| green | 0.170 | 0.797 | 532 nm |
| blue | 0.131 | 0.046 | 467 nm |
sRGB
| x | y | |
|---|---|---|
| red | .64 | .33 |
| green | .30 | .60 |
| blue | .15 | .06 |
P3
| x | y | |
|---|---|---|
| red | .68 | .32 |
| green | .295 | .69 |
| blue | .15 | .06 |
White Point
The white point for all of these color spaces is defined by the D65 spectral power distribution.
D65 xy values in each observer, calculated using CMFs and the d65 spectrum:
| x | y | |
|---|---|---|
| D65 (1931) | 0.3127 | 0.3290 |
| D65 (new) | 0.3134 | 0.3308 |
rec 2020
Because the rec2020 primaries and white point are defined spectrally, we can calculate xy coordinates and a matrix for both the 1931 observer and the updated observer. The wavelength can be directly converted to XYZ by looking up the values in the CMFs.
This plot shows the coordinates of the primaries for rec2020. The 1931 version is dark gray and the new one is light gray.
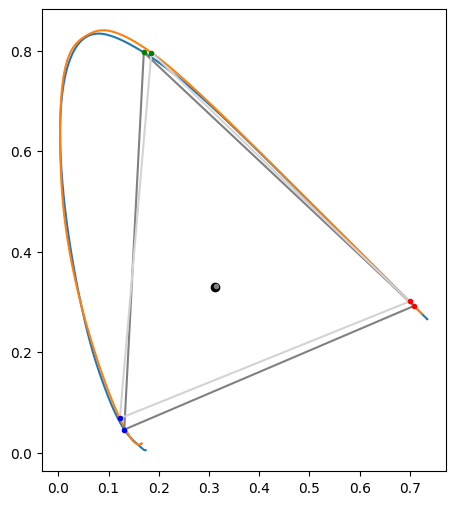
Both are the same color space (same physically, same gamut, and same rgb values) but with different chromaticity coordinates.
The new rec2020 coordinates rounded to 3 digits:
| x | y | |
|---|---|---|
| red | 0.699 | 0.301 |
| green | 0.185 | 0.796 |
| blue | 0.123 | 0.068 |
Spectral RGB primaries
Any rgb color space with spectral or monochromatic primaries can be used with either observer. So rgb values can be converted to different xyz values depending on which version is used.
Redefining RGB primaries
I wanted to find a way to convert XYZ values from the new CMFs to a color space I can actually use like sRGB. I wanted to approximate the new primary colors without having to use spectral measurements of actual displays.
My idea was to use an intermediate rgb color space with monochromatic primaries to convert the xy primary coordinates from one observer to the other. This way the primaries are effectively redefined as relative to a spectral rgb color space.
My process:
- Select wavelengths for red, green, and blue. Convert to xy.
- Use a D65 whitepoint. (or the same as the original color space)
- Make color matrices from the xy values, one set for each cmf (1931, new)
- convert primary xy to xyz
- convert xyz to rgb in the 1931 version of the intermediate color space
- convert rgb to xyz in the new version of the intermediate color space
- convert xyz to xy
- use the new xy coordinates to make a color matrix
Results
Plot showing the result of the transformation. With the coordinates of the original sRGB primaries, the two sets of spectral primaries, and the new “sRGB” primaries.
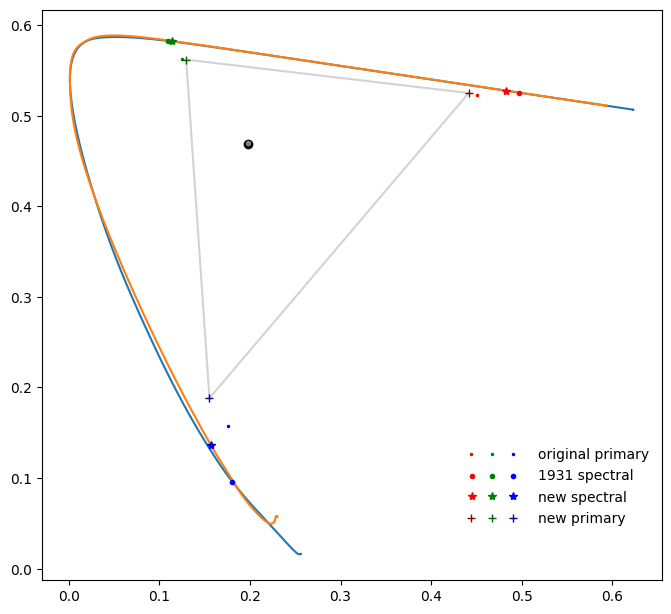
Wavelengths Used
I tested a few combinations of wavelengths including rec2020, and dominant wavelengths of sRGB and P3. I also tried averaging coordinates from a range of wavelengths, but the result was about the same as just using a single wavelength.
# dominant wavelengths
wv_nm = [630, 532, 467] #rec2020
wv_nm = [611, 549, 464] #srgb
wv_nm = [615, 549, 464] #p3
wv_nm = [615, 549, 462] # adjusted blue to 462nm
I used the same values for sRGB and P3 for consistency in profile conversions.
The P3 red primary is spectral, ~615 nm.
The wavelengths for both rec2020 and P3 shift the hue of blue slightly toward purple. Setting the blue wavelength to 462 nm better matches the blue hue in the original 1931 version.
Color Checker Images
Rendered images of the 24-patch Color Checker using the D65 illuminant, with different CMFs and different srgb color matrices.


Comparison of wavelengths
The left side of each color patch is the 1931 color space, the right is the new one.
Mouse-over to swap sides for comparison.



Using the new CMFs with the original sRGB space definitely produces inaccurate colors, showing how XYZ values are incompatible between the two observers. All of the new rgb spaces based on wavelengths come very close to matching the 1931 version.
Which one is more correct? I think it’s impossible to say without spectrally profiling a display. But I would assume that for most colors the 1931 functions are fairly accurate, so trying to match it would probably be best.
Is there any benefit of switching? For most cases, probably not. There should be an advantage when calibrating wider gamut displays, and this method may help with creating a display profile. The channel luminance values (in the table below) seem to be a better estimate of perceived luminance (see below).
My proposed primaries for sRGB and P3 for the new XYZ colorspace
“sRGB like” primaries
| x | y | |
|---|---|---|
| red | 0.636 | 0.336 |
| green | 0.308 | 0.593 |
| blue | 0.141 | 0.076 |
“P3 like” primaries
| x | y | |
|---|---|---|
| red | 0.673 | 0.327 |
| green | 0.305 | 0.683 |
| blue | 0.141 | 0.076 |
White point
| x | y | |
|---|---|---|
| D65 (new) | 0.3134 | 0.3308 |
Comparison of sRGB luminance (Y) values
| R | G | B | |
|---|---|---|---|
| original | 0.2126 | 0.7152 | 0.0722 |
| original (D50 Adapted) | 0.2225 | 0.7169 | 0.0606 |
| new | 0.2228 | 0.6857 | 0.0915 |
Effect of Luminance Values
The 1931 luminance function is known to underestimate the contribution of short wavelengths. This means that for blue colors, the luminance value (as perceived relative to white) is lower than it should be.
While the luminance values are different, the rgb values are very similar. I think the reason this works could be because the brightness of both the blue colors and the display blue primary are underestimated. Your eyes see the display blue as brighter than predicted. The difference gets canceled out and the reproduced color ends up being corrected to the right luminance.
Even though the brightness as displayed is correct, the calculated value is still different. This can matter when profiling a display, calculating grayscale values, or colors of constant luminance. Using a D50 adapted color matrix to calculate luminance (as photoshop grayscale does) adds more error.
Below is a comparison of Oklab ab slices with constant luminance using four different luminance calculations.